Local Manifold Distance

(R) Removing the arch/horseshoe effect in dimensionality reduction methods.

This work has been published with Bioinformatics. Read the full article here.

LMdist for Dimensionality Reduction

Here we give a brief introduction to Local Manifold Distance (LMdist), an algorithm for adjusting pairwise distances in dimensionality reduction in order to remove the “arch effect.”

 

The problem: Arch/Horseshoe Effect

Let’s start with the problem: what is the arch/horseshoe effect?

When conducting dimensionality reduction on big, multivariate datasets, it is common to see the data points form an arch-like formation. It was debated where this was coming from, but most researchers tended to ignore the effect as some “anomaly.”

I found that the arch and horseshoe appear when a gradient is being sampled. So, if the data points are collected along some gradient like temperature, age, pH, or even time. If the ends of the scale are very different from one another, then the arch would appear.

Consider for example this soil dataset, where each dot represents a soil sample taken at a different pH level. The arch is clearly evident, making samples at the ends of the pH gradient appear too close together in the plot. Not representative of the more linear relationship we expect!

 

PCoA plot of Soil microbiome samples with varying pH levels. The closer sample points appear to one another, the more similar their microbiome content. The plot clearly demonstrates an arched shape, not quite the linear pH relationship we would expect.

 

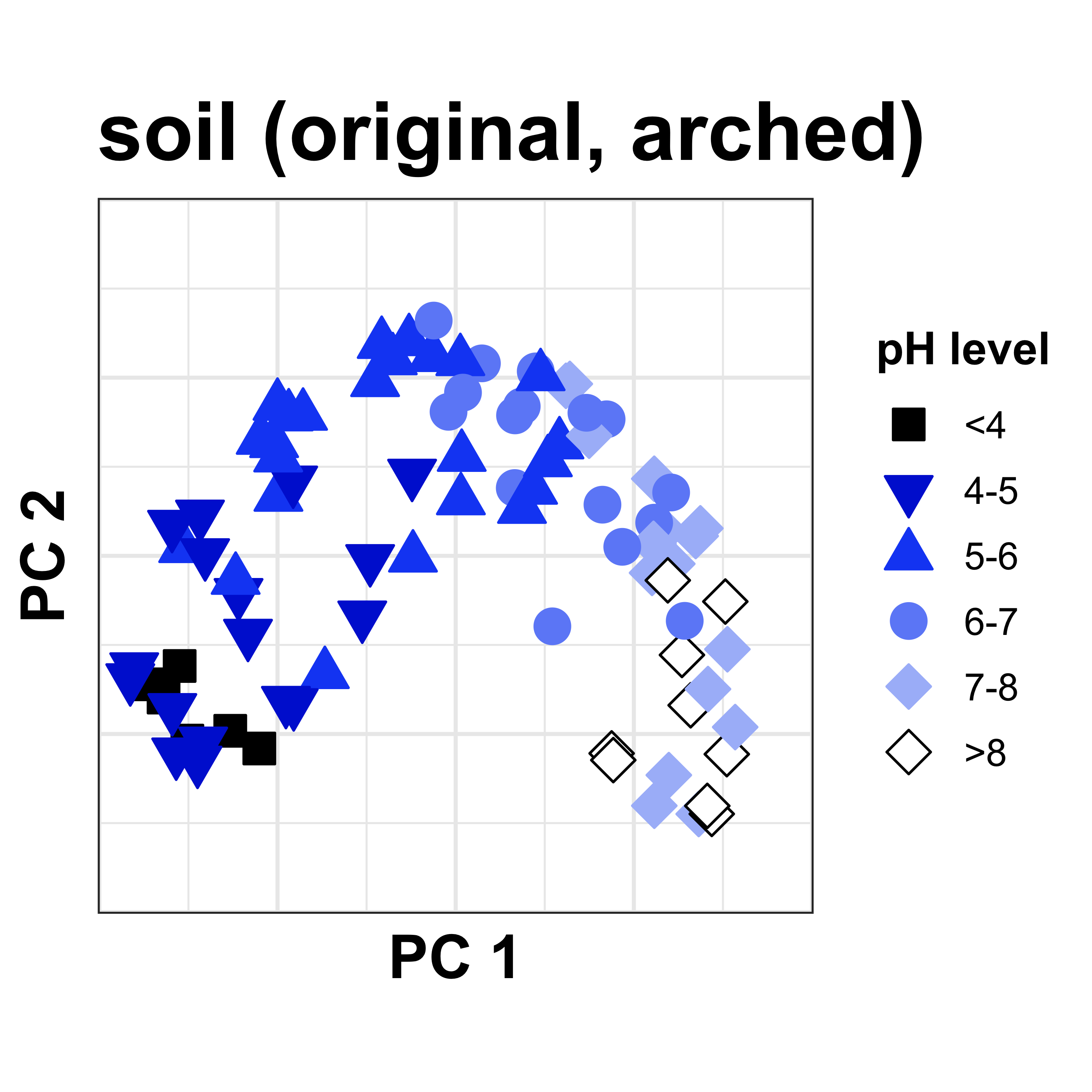
The hypothesis/algorithm: Need adjusted distances

This got me thinking - what if the reason the arch appears with gradients is because the ends of the gradient don’t have much in common? This would affect the pairwise distance measures we use underlying the visualization.

We can use graph theory and machine learning to adjust distances according to local relationships. This will keep short distances the same while making longer distances more accurate for samples at opposite ends of the gradient.

 

A visual representation of the LMdist algorithm. (A) PCoA plot with an arch/horseshoe shape. (B) Given a radius, (C) we connect any other samples within that radius to the sample. (D) We connect neighbors for all samples until we have a fully connected graph. (E) We can recalculate distances by traversing these paths, thereby extending long ditances. (F) Using these adjusted distances as input for dimensionality reduction, we can resolve the linear gradient!

 

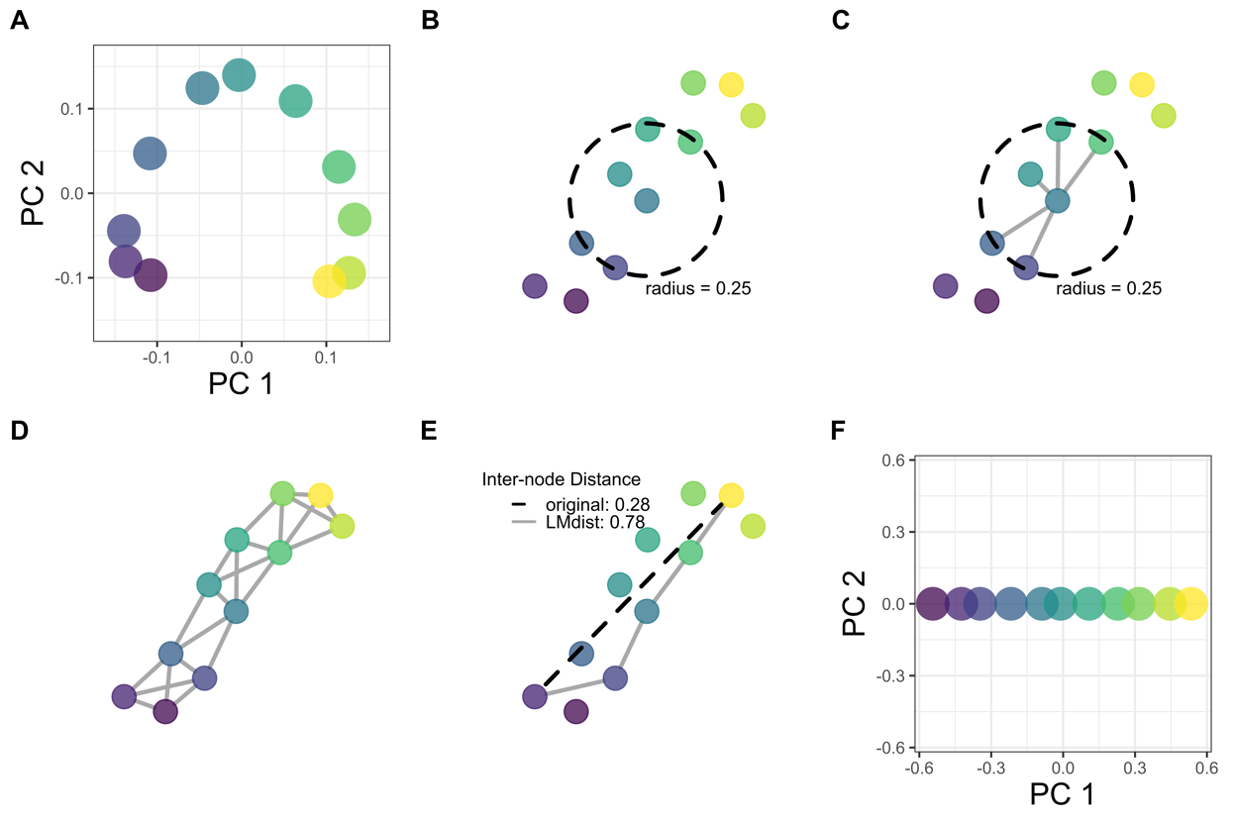
The solution: LMdist recovers gradients

Through verification with a series of simulated datasets, LMdist-adjusted distances more accuarately represent real distances, removing the bounded effect of typical dimensionality reduction approaches.

Applying the LMdist algorithm, we can resolve the pH gradient along the x-axis. This is exciting on its own, but we also find that other variation between the soil samples is now shown in the y-axis direction - meaning we have enabled the discovery of new findings!

 

PCoA plots of the soil samples before (left) and after (right) applying the LMdist algorithm.

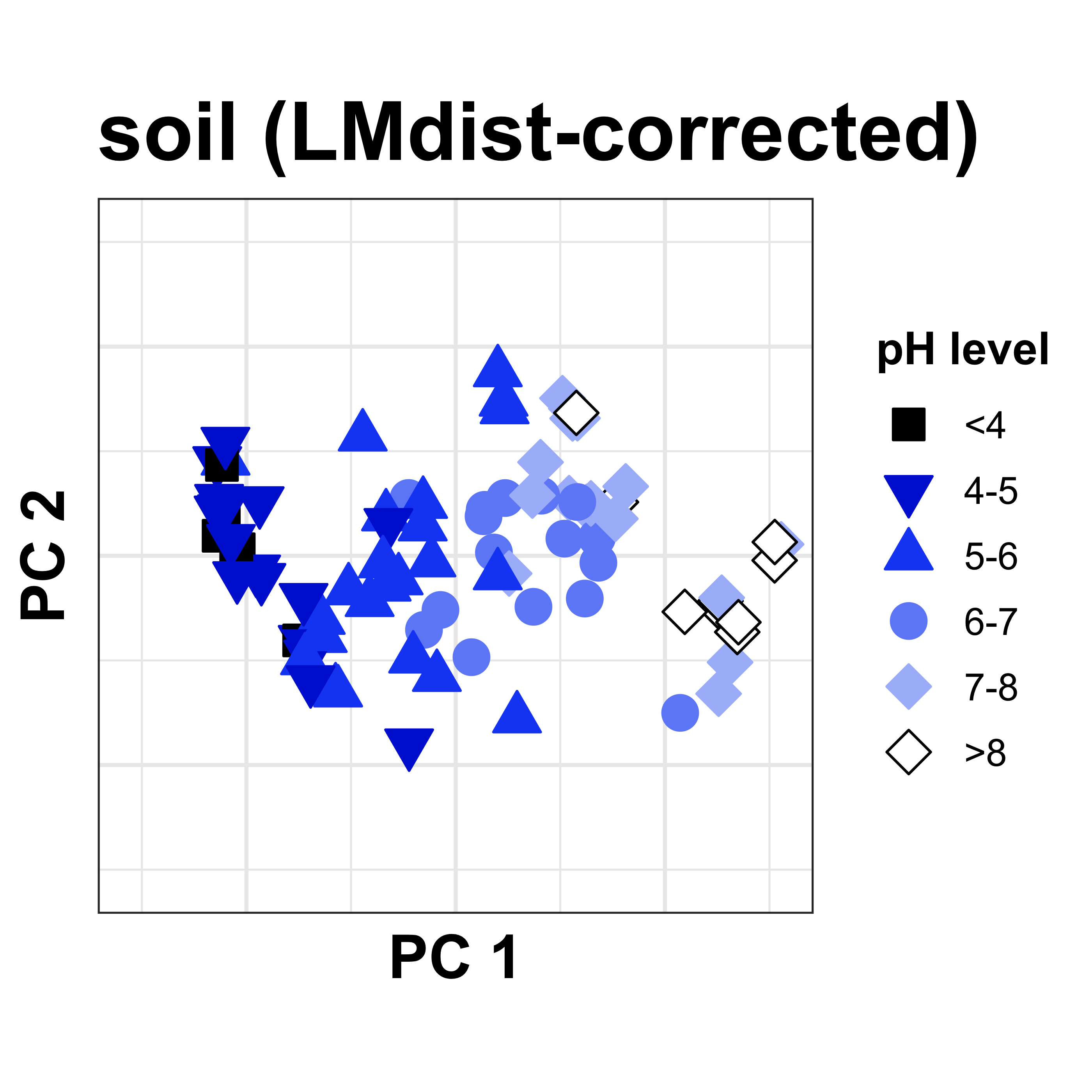
APA citation: Hoops, Susan L., & Knights, Dan (2023). LMdist: Local Manifold distance accurately measures beta diversity in ecological gradients. Bioinformatics, 39(12), btad727.